| Author | Message | ||
Israel |
Why is QT paradoxical?  (Calabi-Yau 3D manifold) (Calabi-Yau 3D manifold) Algebraic Geometry The theory which we call Quantum Mechanics is very strange. Because when we are talking about mechanics it means that we can imagine and see this process visually. But QM came with no visual aids, no model to picture in one's mind. Now this theory is a purely mathematical formalism, difficult to use and impossible to visualize. It simply gives the right answers to the most complicated theoretical question. Such situation satisfy maybe 99% of physicists. But there are few physicists who don’t agree with this situation. They want to understand QT without paradoxes. I consider that these paradoxes are connected with only one reason: " Nobody pays attention to the geometrical form of particles". Now the physicists follow "pure" mathematicians. "Since the mathematical physicists have taken over, theoretical physics has gone to pot. The bizarre concepts generated out of the over use and misinterpretation of mathematics would be funny if it were not for the tragedy of the waste in time, manpower, money, and the resulting misdirection."- - said Richard Feynman. There is difference between "pure" mathematics and the mathematics of theoretical physics. " Pure" mathematics is infinite and the mathematics of theoretical physics is limited by natural laws. The "pure" mathematicians have all rights to create and use abstract models ( point, line …etc) Physicists must use mathematical apparatus in connection with real objects, with real particles. And they forgot about this fact. For example. 1.In thermodynamics particles are "mathematical points", 2. In QT particles are "mathematical points", 3. In SRT, particles are points. But according SRT the "mathematical point", cannot be a firm "mathematical point" . It means it is a "elastic point", which can change its form. (??!!). 4. When this "mathematical elastic point" flies with speed c=1 its form become a flat circle, not a " mathematical point" flying with speed c=1. 5. In QED an electron is an elastic sphere, which can change its form. (??!!). 6. The power, impulse, linear and angular momentum in physics is also a " mathematical point". 7. Then one "mathematical point" /particle/ interacts with another "mathematical point" / power, impulse / the physicists say: " The micro-world is paradoxical." 8. If physicists think about a particle as a " mathematical point" the result can be only paradoxical. And I am sure if somebody takes into consideration the geometrical form of particle the paradoxes of QT will disappear. -------------------------------------------------------------.. P.S. In an Italian railway station: It was more then two hours 'till the departure of the train. I went to the café and ordered a cup of coffee. Soon two men and a very beautiful, slim woman took a place opposite me. They ordered something to drink and one of the man opened a case of violin and took out a bow. He began to explain something about the bow, carefully and gently touching it. Then another man took this bow and also enthusiastically continued this conversation. For half an hour the bow was passed from one hands to another followed with enthusiastic discussion. And the beautiful woman looked at bow and the both these men without saying a word. For half an hour I watched this group with admiration and excitement. What a class! What a cultural level! What a beauty! And now let's imagine the bow pressed into a "mathematical point" and the musicians speak seriously about a "mathematical point" which must produce a sound from a violin. Everybody will say I describe an idiotic situation. Well, I agree. But why doesn't anybody say it to physicists when they observe an elementary particle as a "mathematical point" , without paying attention to its geometrical form. When Feynman said "I think I can safely say that nobody understands quantum mechanics." it was only because nobody took into consideration the geometrical form of a particle. ==================... Best wishes. Israel www.socratus.com (posted via email to humancafe.com) | ||
Israel |
Physics and Geometry. / My opinion./ --------------------. The Classic Physics was started from two points: thermodynamics and light. 1. By studying the effect of thermodynamics, physicists came to the opinion that the physical parameters like volume, temperature and density (of particles mass) are enough to discover the laws of thermodynamics, and they didn’t need to know something concrete about single particle. But then, soon or later, all mass of this particles will stop it’s moving and the thermal/ radiation death will come. Is it possible? No, it isn’t , some particles will radiate and then QT evolved from this idea. Now the situation radically change. From studying mass of particles in thermodynamics Planck and Einstein began to study one individual particle (quantum of energy). It seams that it was logical to think about geometrical form of this particle, but this did not happen. And still now physicists do not think about concrete particles, they are concerned about the “mathematical point”. 2. When physicists studied the behavior of light, they came to the conclusion that light ( light quanta) can sometime be a particle as a “ mathematical point” and sometime a wave as a “ mathematical wave". From behavior of light the SRT was born and here the particle is also “ mathematical point”. It is hard to understand, why nobody think about geometrical form of light quanta if it is real particle. 3. For many years, physicists used Euclidian (static and firm ) geometry for solving physical problems, and they thought there was only one geometry. But Lobachevsky and Bolyai had another opinion. They thought that to use only Euclidian geometry was not enough to explain all the effects in the Universe. Why, because our Universe is not static and firm. The physical processes in Universe change all the time so the Euclidian geometry also has to change. This lead Lobachevsky and Bolyai to discover Non-Euclidian geometry which is not static but elastic. 4. Between the XIX and XX century, many physicists such Abraham, Poincare, Lorentz and Einstein came to the conclusion that the particle (electron) does not have constant mass, energy and length. This means that an electron is not a firm particle. The electron is an elastic particle and therefore his geometrical form can change. All physicists know about this fact and took this fact in their calculations. But which conclusion can be done from this fact? They have no answer. Nobody interested about the borders of this changes. 5. In 1915 Einstein said the mass and speed (moving mass) can change the geometry of space. (GRT). It means the physics without geometry is a limited part of science. It means the physics without geometry is not complete (whole) part of science. 6. The situation we see today is similar to the years between 1900 and 1928 when QT was created. Nothing changes. Mathematicians use Non- Euclidian geometry and they do not know the power of these changes from Euclidian to Non-Euclidian geometry. They do not interested how these changes came. And physicists use forces (energy, impulse, …etc) without know anything about geometrical changes of particles. They do not think about this. For them the particle is only represented by a “mathematical point”. After all, they say the situation in QT is crazy, the Nature is paradoxical. I know why they say this, because one hand “physical” doesn’t know that the other hand “geometrical” does. 7. Can we understand our “ paradoxical” world? The answer is clear. In the Natural world, physics and geometry are one unit part in the evolutionary process, and this fact must be reflected in any future theory of the evolution of matter (as a mass an as a individual particle). 8. There are two ways to reflect this process. One way explained by Einstein in GRT as a man who observed the situation from outside. Another way can be explained by Lobachevsky / Bolyai geometry using it in conjunction with the inner (!) impulse of Planck-Einstein (h) and the inner (!) impulse of Goudsmit – Uhlenbeck (h=h/2pi).. Questions: 1) Where does the Planck/Einstein factor h come from? 2) Where does the Goudsmit / Uhlenbeck factor h=h/2pi come from? 3) What is the physical difference between h and h=h/2pi in the Nature. 4) Can the process of evolution go without geometrical changes? Without the physical/ geometrical theory we cannot answer these questions. -----------------------. And on my opinion, only when we begin to think about light quanta as a particle with a geometrical form we come from image to reality. Best wishes. Israel Sadovnik /Socratus. | ||
Ivan/QT 'time' |
Quantum Theory made 'easy'. In fact, QT is very complex and few truly understand it, though it started from a basic simple premise, that Energy equals the Planck constant times electromagnetic frequency: E=hf. This was the same E=hf in Axiomatic Equation, drawn up against another simple equaltion, E=mc2, to show how gravity is a modified product of such interactions at the quantum level. However, the simplicity ends there, and what follows is exceptionally complex, though also immensely succesful in the real world applications of electronics and computing physics (though not yet for gravity).  Water molecule 'probability' electron shells - from theBigView.com For those of us who are not well versed in the mysteries of QT, and perhaps would like to get a quick thumb sketch of what it's about, visit the 'big view' pages on topics from Relativity to the Uncertainty Principle: the Big View. Here are some quotes from the Space and Time pages:
From Quantum Theory, it says:
But the real issue is the Uncertainty Principle (as posted in the above by Israel), where the BV page says: And earlier on the QT page, it talked about measurement:
But if no 'causality' can be ascribed to the observed, is it the fault of the electron's state in time, or that of the observational limitations in time? Both are questions "in time", and the crux of the dilemma in QT may be this paradox, that time as we understand it at the subatomic level is something else, subject to 'decay' and exists observationally only as a 'probability of time'. Or as Israel said above:
So it's the 'geometry' of time that is in question here. Is Relativistic 'time' the geometry to resolve this Cartesian problem? If the electron is both a wave and particle, geometrically both a point and an event in time, then perhaps how we do our measurements is the problem, rather than the solution... And that makes it 'paradoxical'. But there is no easy solution to this, though the math behind QT makes it usable in our modern technology, and once mastered QT becomes 'easy'. If the quantum 'uncertainty' paradox is an artifact of how an electron diffracted is measured, though mathematically it is correct, then the solution must lie in a better experimental format than used to date. Perhaps gamma ray experiments, with tighter wavelength, would narrow down observational parameters? Ivan Also see: Uncertainty principle not so 'uncertain'... | ||
Ivan/solarcell fractals? Posted From: 69.237.181.12 |
Can fractal geometry be used to improve solar cell efficiency?  (interactive - see: Von Koch curve example) (interactive - see: Von Koch curve example) Fractal pentagram Think how fractal geometry was used to improve cell phone antenna efficiency. So why can't this same idea be used to improve solar panel efficiency in generating electricity from sunlight?  A solar cell silicon wafer (interactive - Wiki solar cells) But how would it work on a relatively flat surface, unless these fractals were somehow integrated beneath the surface? 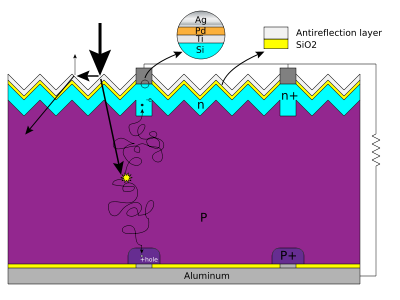 Basic structure of a silicon based solar cell Imagine a crystaline structure within the solar cell that looks like this:  Julia set, or perhaps a Mandelbrot set Or like this:  Animated construction of a Sierpinski Triangle, only going nine generations of infinite. Can it be done to improve solar cell efficiency from the present, say 20-30% where the balance is lost into space, to something more like 50-60% efficiency? Can it be done inside the crystal, for example, where infinity is reduced into these fractal patterns? For that matter, can any "infinite interrelationship" be reduced to its fractal geometry? Something to think about...  An 'infinite' image made by fractal Sterling program: (sin(z) log(z) - tan(z))/(z2 cos(z) 2z) · c Can this fractal geometry be applied to QT? Ivan Also see: Stanford engineers’ optical concentrator could help solar arrays capture more light even on a cloudy day |